Terrestrial Hydrology Model (THM)
Objectives
The most prevalent method of performing hydrologic analysis undoubtedly
involves unit graph theory in which the response to our extended precipitation
event is modelled as the sum of responses to precipitation during each time
interval of the event, without reference to the amount of precipitation
during preceeding or following time intervals. While interest in the rainfall/runoff
process dates back centuries, unit hydrograph theory as it would typically
be applied is approximately one-half century old. There are several weaknesses
associated with unit hydrograph theory. These include:
- Homogeneity - A unit hydrograph is generally applied to a basin
or sub-basin, where it is assumed that the relevant hydrologic parameters
are homogeneous throughout. For this reason, sub-basins or hydrologic response
units should be chosen such that land use, soils, and slopes are relatively
constant throughout. This is often times a very difficult task, as soils
and the landscape in general change from one location to another.
- Linearity - Unit hydrograph procedures operate on the assumption
of linearity. This concept is best illustrated by considering that the unit
hydrograph is essentially a mathematical filter. For a given input precipitation
profile, the output hydrograph is the mathematical convolution of the input
profile with the unit hydrograph. Accordingly, the model's output hydrograph
will respond to the input precipitation in essentially a linear fashion.
Although a real watershed will respond differently to storms of various
magnitudes, this varying response will almost certainly not be linear.
- Timing Parameter - A timing parameter, whether it be time of
concentration, lag time, or time to peak, is required in synthetic unit
hydrograph procedures. This timing parameter is at best difficult to estimate
and often makes little or no reference to the physical properties of the
watershed. The timing parameter effectively controls the timing and peak
of a synthetic unit hydrograph.
The Terrestrial Hydrology Model (THM) being developed as a part of SRBEX
is a raster-based spatially varied model which simulates the surface response
to precipitation in an attempt to over come these weaknesses. This model
utilizes a geographic information systems (GIS) approach to more accurately
represent, both spatially and temporally, the hydrology of a particular
watershed. The main portion of the model is comprised of an infiltration
routine, an overland flow simulation routine, and a channel routing routine.
The user may choose between any of 3 infiltration routines including 1)
a ø-index; 2) the Soil Conservation Service (SCS) curve number technique;
and 3) the solution of the Green-Ampt equation. The model simulates overland
flow on saturated ground via an explicit finite difference solution to
the kinematic wave equations. Channel routing in the model is accomplished
with a form of the Muskingum-Cunge method. Precipitation is supplied to
the model in the form of point rainfall gauges and the coordinates of each
precipitation gauge must be known. Precipitation may be of any time interval
and may contain either cumulative or incremental precipita tion values.
Aside from the precipitation, all other relevant hydrologic information
concerning the landscape is supplied via raster GIS data layers. The model
is capable of estimating all required parameters for successful operation
using the supplied data layers. For instance, the model utilizes empirical relationships for estimating stream channel properties based on drainage
area in order to perform the modified Muskingum-Cunge channel routing operation.
This was done to 1) limit the amount of field data and 2) and to utilize
remotely sensed data.
Results
The THM itself is currently being tested in order to investigate the
sensitivity of the various component parameters and algorithms. Mass
balance testing of the model is complete. The focus now is on simulation
of actual storm events.
Because the THM is capable of simulating a surface response only, a
series of small summer storms which produced rather small, fast peaking
hydrographs was selected in the expectation that these small storms
would be comprised of a limited or negligible amount of return flow from
the saturated zone. The Mahantango Creek Watershed (MCW), a USDA-ARS
research water shed in east-central PA, was chosen as the test
basin. Instrumentation in the MCW includes several meteorological
stations, groundwater monitoring stations, and a multistage weir at the
outlet. For the initial testing, a total of 6 storms was chosen for each
of which all 4 of the available precipitation gauges were active during
the event. For these tests the SCS curve number method was used to
estimate the hydrologic abstractions. Comparisons were made utilizing
all 4 rain gauges as opposed to the temporal average precipitation of
the 4 gauges. The motivation for this was the planned linkage of the THM
and the MM. Since the MM yields only the average precipitation over the
grid cell, it is desirable to understand how the output hydrograph is
affected by assuming uniform precipitation over the grid cell instead of
the actual, spatially varying, precipitation. As testing began, it was
discovered that the initial abstraction term in the SCS method was quite
sensitive. With this in mind, the testing evolved in a slightly
different manner.
Two versions of the experiment were run. In the first, the average
precipitation for the entire test basin was used to calibrate by
comparing the predicted runoff hydrograph to the observed runoff
hydrograph. The literature typically reports values of 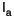 to be approximately 0.2; however,
lower values are often commonplace. An
to be approximately 0.2; however,
lower values are often commonplace. An 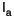 , was calibrated in this manner for each of the 6 test
storms. The calibrated
, was calibrated in this manner for each of the 6 test
storms. The calibrated 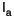 was
then used in investigating the use of the 4 individual gauges (herein
referred to as the spatially varied case) as opposed to an average. In
the second version of the experiment,
was
then used in investigating the use of the 4 individual gauges (herein
referred to as the spatially varied case) as opposed to an average. In
the second version of the experiment, 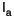 was calibrated for the spatially varied case and used for
the average precipitation case. Both versions gave similar results: for
a given initial abstraction, the spatially varied rainfall of the 4
gauges produced a higher peak than did the average rainfall of the same
4 gauges. This is undoubtedly due to the "smoothing" effect of
mathematical averaging.
was calibrated for the spatially varied case and used for
the average precipitation case. Both versions gave similar results: for
a given initial abstraction, the spatially varied rainfall of the 4
gauges produced a higher peak than did the average rainfall of the same
4 gauges. This is undoubtedly due to the "smoothing" effect of
mathematical averaging.
In the formulation of the kinematic wave approximation for overland flow,
the Manning's "n" or overland flow roughness factor plays an
important role. The more rough the surface, the more the flow is retarded
and hence, the slower the overland velocity. This essentially slows the
travel time of the kinematic wave as it travels down slope. In the current
model, all input describing the earth's surface comes in the form of a gridded
or raster data set. In an effort to avoid an additional data layer describing
the overland flow roughness, a series of "n" values based on the
flow accumulation value of the cell were chosen. The cells with very low
flow accumulation (i.e. the ridge tops) were given a roughness value of
0.4. Cells with a very high flow accumulation value were assumed to be
the agricultural lands and were given an "n" value of 0.12 and
finally, the cells in the middle were given a Manning's "n" value
of 0.20 to 0.25.
In an effort to test the sensitivity of this parameter, a series of model
simulations were made with Manning's "n" values. The Manning's
"n" values ranged between 0.05 and 0.8. For the test runs, all
cells were assigned the same roughness value. The comparisons were made
on the peak flow versus the actual peak as recorded for the event. This
series of simulations indicated that the roughness factor has very little
sensitivity above values of approximately 0.5 with the most sensitive values
being 0.1 and below. The range of recommended roughness values for the conditions
found in the experimental area is 0.05 to 0.4 with most of the basin being
be tween 0.05 and 0.2. The "n" value had considerable impact on
the peak flow within the recommended range; however, when a homogeneous
"n" value anywhere between 0.05 and 0.2 was applied to the basin,
the resulting simulated peak flow was consistently within approximately
25% of the actual recorded peak flow. Interestingly, the "n" value
had limited effect on the timing of the predicted runoff hydrograph.
Overall, the model is able to simulate the 6 storms rather well. The curve
number method has proven to be the most applicable and produces good results.
This is most likely due to the difficulty in estimating and the sensitivity
of the required parameters for the Green-Ampt routine. Investigation of
the Green-Ampt method is continuing.
Future Plans
The addition of several features and algorithms is planned for the
immediate future. These additions include:
- A groundwater or subsurface routine -- It is absolutely
essential to provide a subsurface flow component to the existing
model. This component will enable the analysis and simulation of events
and basins which have substantial return flow components in the
hydrographs. This component is currently under development.
- A reservoir delineation and operation routine -- Because
there are several reservoirs (both controlled and uncontrolled) in the
Susquehanna River basin, it is necessary to model the effects of these
reservoirs if a viable model is to be developed. Current work includes
investigation and development of algorithms to identify reservoirs and
other water bodies through the use of remotely sensed and other spatial
data structures. Additionally, it is intended that the model will
recognize reservoirs and that reservoir operation procedures will become
part of the model.
- Snow melt component -- Although snow melt is normally not a
major consideration in the Susquehanna River basin, the winter of
1993-1994 saw some regions of the basin receiving their largest
snowfalls in history. As a result of this large snowpack, the soil was
saturated for most of the spring melt and heavy rains during this time
resulted in stream flooding. Thus, snowfall had a significant impact on
the basin. A snow melt component is currently being investigated for
addition to the model.
- Additional infiltration routines -- Because of problems
encountered in the existing infiltration routines, additional methods
are being considered.
 Table of Contents
Table of Contents
 Previous Section
Previous Section
 Next
Section
Next
Section
 Download Report
Download Report
Graphics and HTML text markup by Phil Kolb
Comments to: R. White, raw@essc.psu.edu
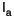 to be approximately 0.2; however,
lower values are often commonplace. An
to be approximately 0.2; however,
lower values are often commonplace. An 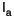 , was calibrated in this manner for each of the 6 test
storms. The calibrated
, was calibrated in this manner for each of the 6 test
storms. The calibrated 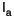 was
then used in investigating the use of the 4 individual gauges (herein
referred to as the spatially varied case) as opposed to an average. In
the second version of the experiment,
was
then used in investigating the use of the 4 individual gauges (herein
referred to as the spatially varied case) as opposed to an average. In
the second version of the experiment, 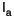 was calibrated for the spatially varied case and used for
the average precipitation case. Both versions gave similar results: for
a given initial abstraction, the spatially varied rainfall of the 4
gauges produced a higher peak than did the average rainfall of the same
4 gauges. This is undoubtedly due to the "smoothing" effect of
mathematical averaging.
was calibrated for the spatially varied case and used for
the average precipitation case. Both versions gave similar results: for
a given initial abstraction, the spatially varied rainfall of the 4
gauges produced a higher peak than did the average rainfall of the same
4 gauges. This is undoubtedly due to the "smoothing" effect of
mathematical averaging. Table of Contents
Table of Contents
 Previous Section
Previous Section
 Next
Section
Next
Section
 Download Report
Download Report