1. ISOCLASS reads the initial cluster center from the statistics
file or assumes that all data are a single cluster
and computes the mean vector and standard deviations of
the data as the first seeding point. The mean vector is
split. (See the heading Splitting Clusters that follows.)
2. Data are assigned to clusters by the minimum distance rule.
The CITYBLOCK distance is used.
3. Cluster means and standard deviations are recomputed. At
the last iteration, covariance matrices are computed.
4. At the PRINTITth iteration, a summary of cluster statistics
is printed.
5. At the VIEWITth iteration, the user is asked if processing
should be interrupted. If so, the next iteration is forced
to be the last iteration.
6. If MAXNUMIT has been reached, the program goes to Step 11.
7. All clusters with fewer than MINCLUST members are deleted.
8. The type of iteration, either split or combine, is
determined. (See the heading Determining Type of Iteration
that follows.)
9. Cluster centroids are split or combined.
10. The program returns to Step 2.
11. Statistics are computed and a summary is printed. The
statistics are stored in OUTSTAT.
12. The image is chained.
The assignment of samples to clusters is done as follows. The data
point x =(x ,x ...x ) is assigned to the Ith cluster if:
k k1 k2 kBANDS
d(x ,m(I)) <= d(x ,m(J)) for all J != I,
k k
--where d(x ,m(I)) is defined as:
k
BANDS
| |
d(x ,m(I)) = SUM | x - m (I) |
k | kj j |
j=1
--and m (I) is the mean for band j of the Ith cluster.
j
Splitting Clusters:
__________________
A cluster is split along the jth coordinate (band) if (1) the jth
coordinate has the maximum standard deviation for the cluster,
(2) the standard deviation along the jth coordinate is greater
than the threshold MAXCLSTD, and (3) the cluster has more than
2(MINCLUST+1) data.
If the previous conditions are met, two new clusters are created
and the parent cluster is deleted. A cluster is created merely
by defining the center (mean) for each coordinate. If the
Ith cluster is split in the jth coordinate, the two new clusters
will have centers at:
(m (I),m (I),...,m (I) + a,...,m (I)) ,
1 2 j BANDS
--and
(m (I),m (I),...,m (I) - a,...,m (I)) ,
1 2 j BANDS
--where a is:
normally, s (I) but can be a constant input by the user (SSEPVAL),
j
--and m (I) is the mean of the jth coordinate of the Ith cluster.
j
On a given split iteration, all clusters that have a standard
deviation greater than MAXCLSTD are split, provided the maximum
number of clusters has not been reached. In that event,
reclassification of the data continues without the creation of
new clusters.
Deleting Clusters:
_________________
All clusters that have fewer than MINCLUST members are deleted. A
cluster is deleted simply by removing the statistics for that
cluster and reducing the number of clusters accordingly.
Combining Clusters:
__________________
Two clusters are combined if the distance between them is less than
the threshold parameter CLUSDIST. The intercluster distance CLD
ij
between clusters I and J is calculated as:
___ ___
| ___ ___ | 1/2
| | 2 | |
| BANDS | (m - m ) | |
| | ki kj | |
CLD = | SUM | ----------- | |
ij | | a a | |
| k=1 | ki kj | |
| |___ ___| |
|___ ___|
--where a is:
ki
normally, s (I) but can be the constant input by the user (SSEPVAL).
k
If CLD < CLUSDIST and CLD < CLD for all m != j and m > i,
ij ij im
--then the clusters I and J are merged to form a new cluster, L,
with means:
N(I)m (I) + N(J)m (J)
k k
m (L) = ---------------------, k=1,...,BANDS
k
N(I) + N(J)
--where N(I) is the total number of data points assigned to
cluster I. The clusters I and J are deleted. The new
cluster, L, is not considered a candidate for merging with
any other cluster on the iteration in which it was found.
Determining Type of Iteration:
_____________________________
The iteration may be a split iteration or a combine iteration. The
sequence of iterations is as follows:
SSSSCSCSC...S
--where:
S = split iteration
C = combine iteration
The beginning sequence of split iterations is terminated when at
least 80 percent of the clusters have standard deviations less
than the threshold parameter MAXCLSTD. At that point, the
iterations alternate between combine and split until the last iteration,
which is always a split iteration.
The initial split iterations are for the automatic initialization
of cluster centers in the event they are not input. The sequence
is shortened considerably if initial cluster centers are input.
Chaining Clusters:
_________________
The last step in the clustering procedure groups all clusters that
have intercluster distances less than CHNTHR, forming one cluster.
The chaining procedure is adopted because the minimum variance
criteria used in the iterative procedure tends to group the data into
spherical (or ellipsoidal) groupings with Gaussian distributions.
This type of grouping is certainly a natural grouping and would
quite often be completely satisfactory. However, there could be
natural groupings of the data that are oddly shaped and cannot be
approximated by Gaussian distributions. Two examples are given in
Figure 1. At the end of the sequence of split and combine
iterations, groupings of the type in Figure 1 are likely to be separated
into clusters as illustrated in Figure 2. The chaining algorithm
groups the clusters 1, 2, and 3 (Figure 2) into one composite
cluster; likewise, clusters 4, 5, 6, and 7 are grouped together to
form one cluster.
The intercluster distances are computed and chaining begins with
the first appearance of two clusters within a distance of CHNTHR
units. Once a cluster is in the chain, all clusters within CHNTHR
units of that cluster are added to the chain. (See example in
Figure 3.)
The statistics (means, standard deviations, and covariance matrices)
of the clusters resulting from chaining are not calculated by the
Gaussian distribution. The cluster assignment image also does not
reflect chaining.
There are, of course, instances in which clusters that are chained
by the program can be safely combined into one composite (Gaussian)
cluster. For example, the three clusters 1, 2, and 3 in Figure 4
can safely be combined into one final cluster. An indication of
such formulas can be used iteratively to compute the composite
statistics.
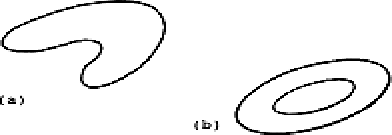
Figure 1. (a) The boomerang-shaped cluster
(b) The donut-shaped cluster

Figure 2. Breaking up of the clusters (a) and (b) of
Figure 1 into subclusters
(a)

(b)
\\ I |
J \\ | 1 | 2 | 3 | 4 | 5
__________|_______|_______|_______|_______|_______
1 | 0.0 | 7.5 | 6.2 | 3.2 | 11.8
2 | 7.5 | 0.0 | 3.1 | 5.6 | 3.0
3 | 6.2 | 3.1 | 0.0 | 3.1 | 6.2 DLMIN=3.2
4 | 3.2 | 5.6 | 3.1 | 0.0 | 9.7
5 | 11.8 | 3.0 | 6.3 | 9.7 | 0.0
Figure 3. Example of Chaining:
(a) Cluster structure
(b) Intercluster distance table

Figure 4. An example in which the chained subclusters can
safely be combined into one composite cluster.
Assuming that two clusters {n1,m1,C1} and {n2,m2,C2} are considered
as one cluster {n,m,C}, where n's, m's, and C's are, respectively,
the number of points, mean vectors, and covariance matrices, then:
n = n + n
1 2
n n
1 2
m = ------- m + ------- m
n + n 1 n + n 2
1 2 1 2
n n
1 2
C = ------- C + ------- C
n + n 1 n + n 2
1 2 1 2
n n
1 T 2 T T
+ ------- m m + ------- m m - mm
n + n 1 1 n + n 2 2
1 2 1 2
The user should be cautious about the values of CLUSDIST and MAXCLSTD in
the combine and split routines. The range of values 3.2-3.9 for
CLUSDIST have been established in connection with the probability of
misclassification. Values outside this range are discouraged. Of
course, values of CLUSDIST closer to the lower bound will induce finer
groupings, while larger values will induce coarser groupings.
As to the value of MAXCLSTD, its value directly governs the size of nominal-sized clusters. For data collected by multispectral scanners, a MAXCLSTD value of 4.5 is suggested. Higher values of this threshold are acceptable, e.g., 6.0 and 7.0, inducing coarser groupings.
The statistics of each cluster are written to the statistics file named in OUTSTAT. OUTSTAT is a new file every time. ISOCLASS names the classes as CLUSTO1, CLUSTO2, etc. The user may start ISOCLASS again using the statistics file from the previous ISOCLASS execution as input and can continue the iterations from there.